一、素数
欧拉筛
void prime(){ check[1]=1; for(int i=2;i<=n;i++){ if(!check[i])prim[++cnt]=i;//这个if语句后面没有大括号!! for(int j=1;j<=cnt&&prim[j]*i<=n;j++){ check[i*prim[j]]=true; if(i%prim[j]==0)break; } }} 简单的素数判定
bool check(int x){ if(x<=1)return false; for(int i=2;i*i<=x;i++) if(x%i==0)return false; return true;} 搜索+素数判定
二、欧几里得+扩展欧几里得
欧几里得
int gcd(int x,int y){ return y==0?x:gcd(y,x%y);} 多组gcd预处理
#include#include using namespace std;int n,m,g[100][100];int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ g[i][i]=i;g[i][0]=g[0][i]=i; for(int j=1;j
扩展欧几里得
求逆元:当一个数与它的模数m互质时,那么它在模m意义下的逆元为
这个数的m-2次方。
void exgcd(int a,int b,int &x,int &y){ if(b==0){ x=1;y=0; return a; } int r=exgcd(b,a%b,x,y),t; t=x;x=y;y=t-a/b*y; return r;}gcd=exgcd(a,b,x,y);if(gcd!=1)printf("不存在\n")while(x<=0)x+b/gcd; 三、欧拉函数
phi(n)为小于等于n且与n互质的数的个数。
int get_phi(int x){ int sum=x; if(x%2==0){ while(x%2==0)x/=2; sum/=2; } for(int i=3;i*i<=x;i+=2){ if(x%i==0){ while(x%i==0)x/=i; sum=sum/i*(i-1); } } if(x>1)sum=sum/x*(x-1); return sum;} hzwer的
int phi(int n){ int ans=n; for(int i=1;pri[i]<=sqrt(n);i++) if(n%pri[i]==0) { ans=(ans-ans/pri[i]); while(n%pri[i]==0)n/=pri[i]; } if(n!=1)ans=(ans-ans/n); return ans%K;} int euler(int n){ //返回euler(n) int res=n,a=n; for(int i=2;i*i<=a;i++){ if(a%i==0){ res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出 while(a%i==0) a/=i; } } if(a>1) res=res/a*(a-1); return res; } 四、卡特兰数
不想写了....博客会陆续写几道题的....
去分类里找吧。谢谢滋瓷(。・・)ノ
五、中国剩余定理
设m1,m2,m3,m4两两互素,则同余方程组 x≡a1(m1) x≡a2(m2) x≡a3(m3) x≡a4(m4) .... x≡ak(mk) 一定有解,x≡(a1*M1*M1^(-1)+a2*M2*M2^(-1)+....) 其中M=m1*m2*...*mk,Mi=M/mi,Mi^(-1)是Mi在模mi意义下的逆元。 普通的中国剩余定理要求所有mi互素,那么如果不互素呢? 我们采用两两合并的思想,假设要合并如下两个方程 x=a1+m1*x1 x=a2+m2*x2 那么得到 a1+m1x1=a2+m2x2 => m1x1+m2x2=a2-a1 再利用扩展欧几里得算法解出x1的最小正整数解,再带入 x=a1+m1x1,得到x后合并为一个方程的结果过为 y≡x(mod lcm(m1,m2)) 这样一直合并下去,最终可以求得同余方程的解。 模板:互素的
#include#include #include using namespace std;int a[4],m[4];int p,e,i,d,t=1;void exgcd(int a,int b,int &x,int &y){ if(b==0){ x=1; y=0; return; } exgcd(b,a%b,x,y); int tmp=x; x=y; y=tmp-(a/b)*y;}int CRT(int a[],int m[],int n){ int M=1,ans=0; for(int i=1;i<=n;i++)M*=m[i]; for(int i=1;i<=n;i++){ int x,y; int Mi=M/m[i]; exgcd(Mi,m[i],x,y); ans=(ans+Mi*x*a[i])%M; } if(ans<0)ans+=M; return ans;}int main(){ while(cin>>p>>e>>i>>d){ if(p==-1&&e==-1&&i==-1&&d==-1)break; a[1]=p;a[2]=e;a[3]=i; m[1]=23;m[2]=28;m[3]=33; int ans=CRT(a,m,3); if(ans<=d)ans+=21252; printf("Case %d: the next triple peak occurs in %d days.\n",t++,ans-d); } return 0;}
不互素的
#include#include #include #include #include #define N 5#define ll long long using namespace std;ll n,m[N],a[N],m1,e;ll read(){ ll x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){ if(ch=='-')f=-1; ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} return x*f;}ll exgcd(ll a,ll b,ll &x,ll &y){ if(b==0) { x=1,y=0; return a; } ll r=exgcd(b,a%b,x,y),tmp; tmp=x,x=y,y=tmp-a/b*y; return r;}ll crt(){ ll a1=a[1],a2,m2,d,c;m1=m[1]; for(ll i=2;i<=n;++i) { a2=a[i],m2=m[i]; c=a2-a1;ll x=0,y=0; d=exgcd(m1,m2,x,y); if(c%d) return -1; x=x*c/d; int mod=m2/d; x=(mod+x%mod)%mod; a1+=m1*x;m1*=mod; } return a1;}int main(){// freopen("mod.in","r",stdin);// freopen("mod.out","w",stdout); n=4; for(int i=1;i<=n;i++) m[i]=read(),a[i]=read(); printf("%lld\n",crt()); return 0;}
六、斐波那契
递推公式:f[i]=f[i-1]+f[i-2],f[1]=f[2]=1
通项公式:
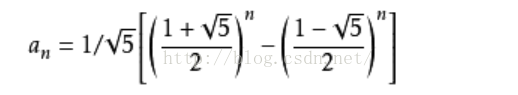
矩阵乘法求斐波那契:
A:(F[i−1]F[i])。B=(01)
(11)
两个矩阵乘一乘就好啦。
重要定理:gcd(f[n],f[m])=f[gcd(n,m)]
七、排列组合
排列公式:
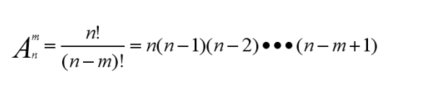
组合数公式:
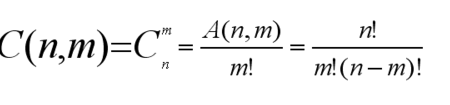
递推法求组合数
for(int i=0;i<=k;i++) { for(int j=0;j<=i;j++) { if(j==0) c[i][j]=1; else if(i==j) c[i][j]=1; else c[i][j]=(c[i-1][j]%M+c[i-1][j-1]%M)%M; } }
如果是计算C(n,m)%p,p是个素数,那么n!/(m!*(n-m)!)=n!*(f[m]*f[n-m])^(p-2)
f[m]为m的阶乘。
Lucas定理:用于大组合数取模问题

插板法:不想多说...来个吧...
十、错排
错排:考虑n个元素的一个排列,若每个元素都不在原来的位置,那么这个
排列就叫做原来排列的一个错排。
错排公式:f[i]=(f[i-1]+f[i-2])*(i-1)
错排通项公式:f[n]=n!*[(-1)^2/2!+(-1)^3/3!+(-1)^4/4!+...+(-1)^n/n!]
十一、容斥原理
容斥原理是一种重要的组合数学的方法,可以让你求解任意组的大小,或者
计算复合事件的概率。
要计算几个集合合并的大小,我们要先将单个集合计算出来,然后减去所有
两个集合相交的部分,再加回所有三个集合相交的部分,再减去所有四个集合
相交的部分。依此类推.....

几个例题:
(1)简单排列问题
0--9组成的排列,要求第一个数字大于1,最后一个数小于8,共有几个排列。
首先算出第一个元素小于等于1(有x种排列)或者最后一个元素大于等于8
(有Y种排列),通过容斥原理写成:
|X|+|Y|-|X∩Y|。经过计算可以写成:
2*9!+2*9!-2*2*8! 就是所有不满足条件的情况,再用总排列10!减去就是答案了。
(2)序列问题
长度为n的由数字0,1,2组成的序列,要求每个数字至少出现1次,这样的序列有
多少种?
定义Ai为不出现数字i的序列数,那么通过容斥原理,我们得到该逆问题的结果为:
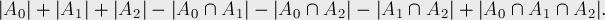
可以发现
每个Ai值都是2^n,而所有两两组合的Ai∩Aj都为1,最后三个集合的交集为0;
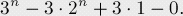
其他没什么好说的,贴上几个题吧。